CSAPP要点总结 第2章 信息的表示和处理 part3 浮点数
整数和浮点数的表示是不同的,
整数是精确的,浮点数是近似的。
整数防止溢出,整数具有加法、乘法的结合律
然而浮点数不具有结合律,因为浮点是近似的。
定点数
略
IEEE浮点表示
浮点数最重要的标准是IEEE 754标准 IEEE浮点标准用 $V = (-1)^s \times M \times 2^E$的形式表示,
s代表符号位,只有1位,s=1表示负数,s=0表示正数。 M代表尾数,范围[1, 2) 或者 [0, 1) E代表阶码,
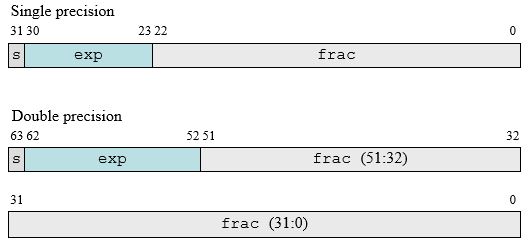
对于单精度,s = 1(第31位), M = 8(第23到30位), E = 23(第0到22位) 对于双精度,s = 1(第63位), M = 11(第52到62位), E = 52(第0到51位) 如下图所示:
对于浮点数还分成了三类,分别用于不同场合的浮点数表示, 如下图所示:
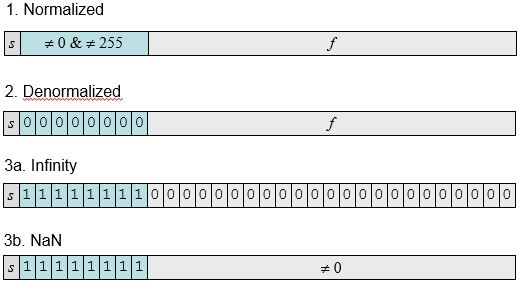
1) 规格化的值(normalized value)
即当exp的位不全为0且不全为1(单精度对应8位 255、双精度对于11位 2047)时,如上图。
符号位 s
对于符号位不用说了。
阶码段
对于阶码E, E = e - Bias, 其中e即阶码段上的无符号数, 例如单精度8位,那么取值范围就是 1 ~ 2^8-1 -1 = 254, (注意不能是0和255) 对于双精度11位,那么同理取值范围是 1 ~ 2^11-1 -1 = 2046 (注意不能是0和2047)
为了同时表示负数的情况,于是通过Bias偏置掉一半的数,
$Bias = 2^{k-1}-1$,于是:
对于单精度即 2^7 - 1 = 127,因此分水岭E=0发生在二进制为0111 1111
对于双精度即 2^10 - 1 = 1023,因此分水岭E=0发生在二进制为011 1111 1111
因此,E的取值范围单精度为 -126~127,双精度为 -1022~1023
小数段
对于小数段,隐含以1开头(implied leading 1), 即 1 + f,取值范围 [1, 2) 当frac段全为0时,可以取1,但全为1也没法到2。 最小值对于单精度和双精度都是1.0 最大值对于单精度是 $ 1 + 1 - \frac{1}{2^{23}} \approx 1.999 999 880 790 71$,精度约为$ 10^{-7} $ 对于双精度是 $ 1 + 1- \frac{1}{2^{52}} $
取值范围小结
综上可知,对于规格化的值,其取值范围为:
以单精度最大/小值为例: 0/1 | 1111 1110 | 111 1111 1111 1111 1111 1111 即 $\pm$ 1.999 999 880 790 * 2^127
最小norm的值: 0/1 | 0000 0001 | 000 0000 0000 0000 0000 0000 即 $\pm$ 1.0 * 2^-126
2) 非规格化的值(denormalized value)
简单说,就是为了表示0.0
符号位 s
需要说明的是,根据IEEE的浮点格式,+0.0和-0.0在某些方面是不同的,其他方面是相同的。
阶码段
对于阶码E, E = 1 - Bias, (如果按照norm的方式则为 0 - Bias) 因此对于单精度,E = 1 - 127 = -126 E之所以这样做,主要是为了平滑得从最小norm值过渡到denorm值 例如对于单精度,norm最小值为 1.0 * 2^-126,而denorm最大值为0.999 999 880 790 * 2^-126
小数段
对于小数段,不同于规格化数,并不隐含以1开头,而是以0开头, 即 f,取值范围 [0, 1) 当frac段全为0时,可以得到0,但全为1也没法到1。 最小值对于单精度和双精度都是0.0 最大值对于单精度是 $ 1 - \frac{1}{2^{23}} \approx 0.999 999 880 790 71$ 对于双精度是 $ 1- \frac{1}{2^{52}} $
取值范围小结
问题来了,为什么当exp段全为0的时候要突然从norm转到denorm呢? 为什么不都按照norm的规则呢? 答: 以单精度为例, 对于denorm的精度(即除了0以外的最小值) 0/1 | 0000 0000 | 000 0000 0000 0000 0000 0001 2^-23 * 2^-126,最小值为0 如果采用norm的方式,最小值为 E = 1.0*2^-127,不能表示0.0, 当然,其精度可以达到2^-23 * 2^-127。 所以可以发现,之所以要考虑非规格化的值,是因为为了表示0.0 为了表示0,我们舍弃掉norm本可表示的最高精度2^-127,而把后面的空间拉平,表示了零,精度降一半。
规格化数和非规格化数的分布
值得说明的是非规格化数是均匀分布的,且自然过渡到规格化数。 而规格化数不是,如下图:
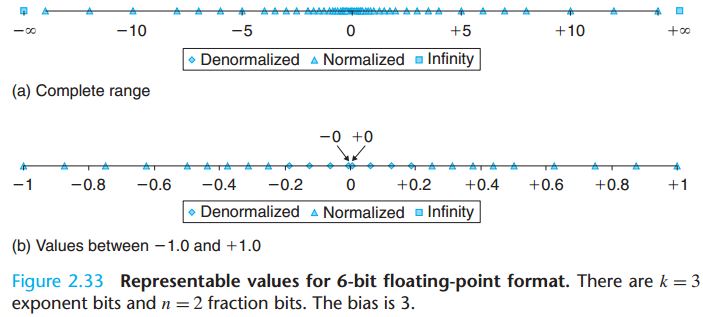
这是因为对于规格化数,每当E幂指数+1,精度则减少一半。 对于单精度,规格化数的最小精度为 2^-23 * 2^-126 而非规格化数 E=1,相当于fixed number,精度始终为2^-23 * 2^-126
3) 特殊值
当exp全为1时,若frac全为0,表示$\pm \infty$ 可用于除以0或者溢出的场合。
当exp全为1时,而frac不为0,表示NaN,当一个运算不能为实数或无穷时, 例如:$\sqrt[2]{-1}$ 或者 $\infty - \infty$,也可在某些应用中表示未初始化的数,很有用。
IEEE浮点数取值范围
可以看到: 对于单精度,可表示最小精度是 $1.4 \times 10^{-45}$,最大值是 $3.4 \times 10^{38}$ 对于双精度,可表示最小精度是 $4.9 \times 10^{-324}$。最大值是 $1.8 \times 10^{308}$

舍入
IEEE浮点数格式定义了4种不同舍入方法, 默认是round-to-nearest,除了0.5这个数字外其他是就近原则, 0.5是舍入到最近的偶数,例如1.5和2.5都舍入到2,所以也称为round-to-even
其他三种方式产生实际值的确界(guaranteed bound),在一些数字应用中比较有用。
round-toward-zero将正数、负数都朝着0舍入。 round-to-down,也可称为floor函数吧,向下舍入。 round-to-up,也可称为ceiling函数,向上舍入。
之所以考虑偶数舍入,是为了减少统计情况下向同一边舍入带来的偏差。
浮点运算
前面知道,整数加法构成了阿贝尔群,其实,实数加法也构成阿贝尔群。 然而,实数加法可以交换,但不满足结合律! 例如: (3.14 + 1e10) - 1e10 = 0.0,而3.14 + (1e10 - 1e10) = 3.14
作为阿贝尔群,实数加法到多数值存在逆元 -x, 但是 $\infty$ 和 NaN是例外,因为$\infty - \infty = NaN$而不是0。
因为不满足结合律,所以编译器在优化时,偏向于保守, 很多看似可优化的,因为不知道作者是否在意结合律性来的可能不大的误差,所以没有优化。
另外,实数加法满足单调性,即若 $a \geq b$ 则 $ a + x \geq b + x $。 然而对于整数,由于存在溢出的情况,不满足单调性。
对于乘法,也是满足交换律,但不满足结合率,且不满足分配律。
对于程序员而言,不满足结合律和分配律是很严重的。
C语言中的浮点数
C提供两种浮点是,float和double且大多情况下支持IEEE标准, 但C并没有强制要求符合IEEE标准,因此并没有标准方法改变舍入方式或者定义诸如-0, $+\infty$, $-\infty$或者NaN这些特殊值, 大多数系统提供相应头文件或库,但没有统一标准,可能细节有所不同。
强制转换的规则:
- 从int到float,数字不会溢出,但可能被舍入。
- 从int/float转到double,因double精度更大,因此能保留精确的数值。
- 从double到float,可能溢出成为 $\pm \infty$,也有可能因精度问题被舍入
- 从float/double转为int,值将向零舍入。进一步说,值可能会溢出(毕竟浮点数范围更大)。然而,C标准没有对此的规定。因此,有些诸如与Intel兼容的微处理器将整数最小值统一定义为整数不确定(integer indefinite)值,即溢出结果。例如对于32位数,TMin_32 = [10…000] = -2^31 = 2 147 483 648。
问题来了,将int转为float类型在什么情况下需要舍入? 答: 首先,在精度大于1的情况下才会出现需要舍入的情况, 这个数是: 1/0 | 移23位,即 1001 0101 | 111 1111 1111 1111 1111 1111 这个数换2进制是: 1111 1111 1111 1111 1111 1111,即2^24 -1 = 16 777 215。 2^24也可以正确表示,但是2^24 + 1 将没有浮点数精确表示,需要舍入。 而对于double因为frac段就已经超过32位了,带到52位,根据不担心是否需要舍入。
注意:将大的浮点数转换成整数是一种常见的程序错误。
